Hybrid Models

Models that are a hybrid of the boundary manikin and population model techniques are robust tools to determine appropriate adjustability of a device for a desired level of accommodation. Hybrid models often yield better results than either manikin or population techniques alone. Hybrid models were introduced to the DfHV field in the early 2000’s, as the importance of preference and modeling real user behavior became recognized (see Reed, 2000 and Parkinson, 2005).

Hybrid models combine the experimental nature of population models with the statistical nature of manikin-based design. A simple implementation of a hybrid model works like this:

1. Create a prototype of the device being designed. This prototype should have ample adjustability in the dimension(s) under consideration.
2. Gather a relatively small sample of experimental participants, and determine how the experiment will be conducted.
3. Take relevant measurements of the sample population. Stature and BMI are easy to measure and are almost always collected, but other measurements specific to the problem may also need to be obtained.
4. Run an experiment in which each person in the sample population uses the prototype. Record user’s selected setting(s).
5. Create a regression model of the data that correlates users’ settings with one or more measures of their anthropometry.
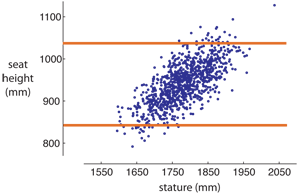
6. Enter appropriate limits of anthropometry (5th and 95th percentile stature, for example) into regression equation, to get limits of the device’s range of adjustment for desired level of accommodation. See figure below for a sample population, regression line, and adjustment limits in orange determined by 2.5th and 97.5th stature of the target population under consideration.

More advanced implementations of hybrid models use not only the linear component of the regression, but also retain a measure of scatter (e.g., root mean squared error, RMSE). This measure of scatter is used to add a stochastic component to the simulations that represents user preference. An implementation of a hybrid model works like this (starting with step 5 above):

1. Create a virtual population of a large number of people (e.g., 1000). Randomly sampling the given number of people from an existing anthropometric database (e.g., ANSUR) is one way to accomplish this.
2. Using the regression equation from step 5 above, determine the preferred device setting for each person. This equation should include not only the mean location predicted by the slope and intercept of the regression, but should also add a random component generated by sampling random values from a normal distribution with standard deviation equal to the RMSE of the regression.
3. Determine limits for the design by selecting cutoffs that accommodate the desired percentage of target users. For example, to accommodate 95% of users, set the device adjustment cutoffs so that the central 950 of 1000 users are accommodated. See figure below for a sample virtual population of 1000 people created from the regression above, and adjustment limits in orange to accommodate the central 950.

While hybrid models offer more accurate results than manikin or population models, they require both an experiment and statistical analysis, and therefore cost more time and money. See Garneau, 2007 for a more thorough discussion of this procedure and a sample case study of the method applied to the design of an exercise seat cycle.